Skip to content

NumPy for Machine Learning

View all lessons
Numerical analysis with the NumPy computing package.
Goku Mohandas
Goku Mohandas
· · ·
Repository · Notebook

📬  Receive new lessons straight to your inbox (once a month) and join 30K+ developers in learning how to responsibly deliver value with ML.

Set up

First we'll import the NumPy package and set seeds for reproducibility so that we can receive the exact same results every time.

1
import numpy as np

1
2
# Set seed for reproducibility
np.random.seed(seed=1234)




Basics



tensors



1
2
3
4
5
6
7
# Scalar
x = np.array(6)
print ("x: ", x)
print ("x ndim: ", x.ndim) # number of dimensions
print ("x shape:", x.shape) # dimensions
print ("x size: ", x.size) # size of elements
print ("x dtype: ", x.dtype) # data type





x:  6
x ndim:  0
x shape: ()
x size:  1
x dtype:  int64



1
2
3
4
5
6
7
# Vector
x = np.array([1.3 , 2.2 , 1.7])
print ("x: ", x)
print ("x ndim: ", x.ndim)
print ("x shape:", x.shape)
print ("x size: ", x.size)
print ("x dtype: ", x.dtype) # notice the float datatype





x:  [1.3 2.2 1.7]
x ndim:  1
x shape: (3,)
x size:  3
x dtype:  float64



1
2
3
4
5
6
7
# Matrix
x = np.array([[1,2], [3,4]])
print ("x:\n", x)
print ("x ndim: ", x.ndim)
print ("x shape:", x.shape)
print ("x size: ", x.size)
print ("x dtype: ", x.dtype)





x:
 [[1 2]
 [3 4]]
x ndim:  2
x shape: (2, 2)
x size:  4
x dtype:  int64



1
2
3
4
5
6
7
# 3-D Tensor
x = np.array([[[1,2],[3,4]],[[5,6],[7,8]]])
print ("x:\n", x)
print ("x ndim: ", x.ndim)
print ("x shape:", x.shape)
print ("x size: ", x.size)
print ("x dtype: ", x.dtype)





x:
 [[[1 2]
  [3 4]]

 [[5 6]
  [7 8]]]
x ndim:  3
x shape: (2, 2, 2)
x size:  8
x dtype:  int64



NumPy also comes with several functions that allow us to create tensors quickly.

1
2
3
4
5
# Functions
print ("np.zeros((2,2)):\n", np.zeros((2,2)))
print ("np.ones((2,2)):\n", np.ones((2,2)))
print ("np.eye((2)):\n", np.eye((2))) # identity matrix
print ("np.random.random((2,2)):\n", np.random.random((2,2)))





np.zeros((2,2)):
 [[0. 0.]
 [0. 0.]]
np.ones((2,2)):
 [[1. 1.]
 [1. 1.]]
np.eye((2)):
 [[1. 0.]
 [0. 1.]]
np.random.random((2,2)):
 [[0.19151945 0.62210877]
 [0.43772774 0.78535858]]



Indexing


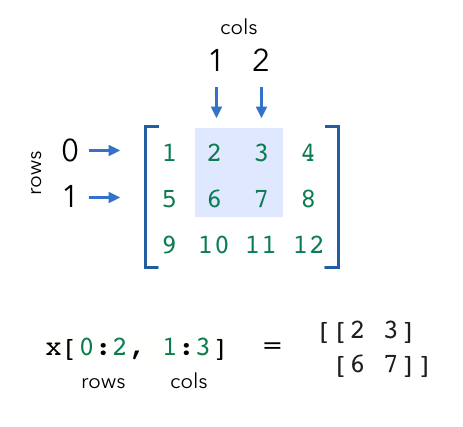
We can extract specific values from our tensors using indexing.




Keep in mind that when indexing the row and column, indices start at 0. And like indexing with lists, we can use negative indices as well (where -1 is the last item).





numpy indexing



1
2
3
4
5
6
# Indexing
x = np.array([1, 2, 3])
print ("x: ", x)
print ("x[0]: ", x[0])
x[0] = 0
print ("x: ", x)





x:  [1 2 3]
x[0]:  1
x:  [0 2 3]



1
2
3
4
5
6
# Slicing
x = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
print (x)
print ("x column 1: ", x[:, 1])
print ("x row 0: ", x[0, :])
print ("x rows 0,1 & cols 1,2: \n", x[0:2, 1:3])





[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]
x column 1:  [ 2  6 10]
x row 0:  [1 2 3 4]
x rows 0,1 & cols 1,2:
 [[2 3]
 [6 7]]



1
2
3
4
5
6
7
8
# Integer array indexing
print (x)
rows_to_get = np.array([0, 1, 2])
print ("rows_to_get: ", rows_to_get)
cols_to_get = np.array([0, 2, 1])
print ("cols_to_get: ", cols_to_get)
# Combine sequences above to get values to get
print ("indexed values: ", x[rows_to_get, cols_to_get]) # (0, 0), (1, 2), (2, 1)





[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]
rows_to_get:  [0 1 2]
cols_to_get:  [0 2 1]
indexed values:  [ 1  7 10]



1
2
3
4
5
# Boolean array indexing
x = np.array([[1, 2], [3, 4], [5, 6]])
print ("x:\n", x)
print ("x > 2:\n", x > 2)
print ("x[x > 2]:\n", x[x > 2])





x:
 [[1 2]
 [3 4]
 [5 6]]
x > 2:
 [[False False]
 [ True  True]
 [ True  True]]
x[x > 2]:
 [3 4 5 6]



Arithmetic


1
2
3
4
5
6
# Basic math
x = np.array([[1,2], [3,4]], dtype=np.float64)
y = np.array([[1,2], [3,4]], dtype=np.float64)
print ("x + y:\n", np.add(x, y)) # or x + y
print ("x - y:\n", np.subtract(x, y)) # or x - y
print ("x * y:\n", np.multiply(x, y)) # or x * y





x + y:
 [[2. 4.]
 [6. 8.]]
x - y:
 [[0. 0.]
 [0. 0.]]
x * y:
 [[ 1.  4.]
 [ 9. 16.]]



Dot product


One of the most common NumPy operations we’ll use in machine learning is matrix multiplication using the dot product. Suppose we wanted to take the dot product of two matrices with shapes [2 X 3] and [3 X 2]. We take the rows of our first matrix (2) and the columns of our second matrix (2) to determine the dot product, giving us an output of [2 X 2]. The only requirement is that the inside dimensions match, in this case the first matrix has 3 columns and the second matrix has 3 rows.



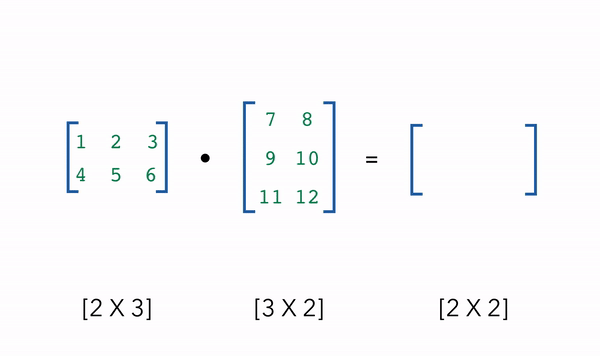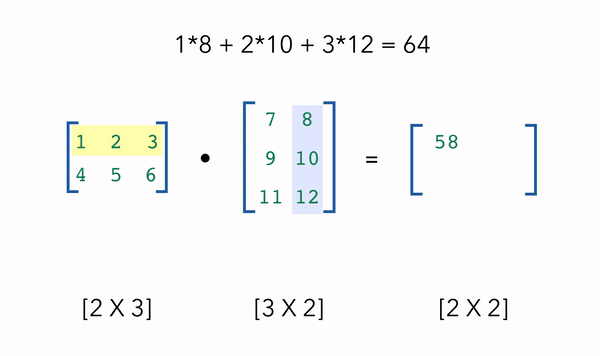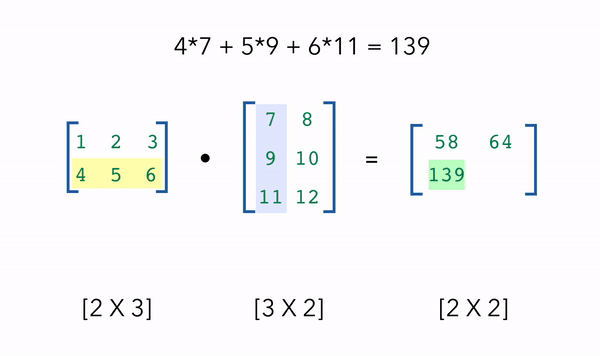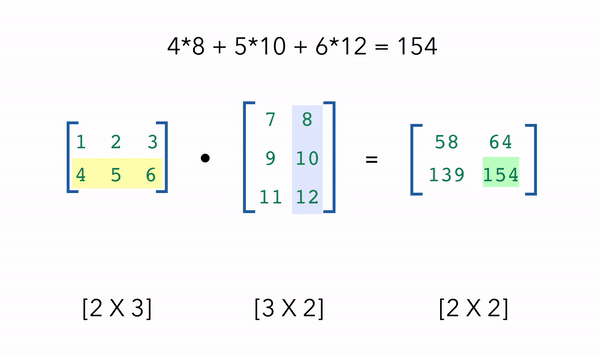
dot product



1
2
3
4
5
6
# Dot product
a = np.array([[1,2,3], [4,5,6]], dtype=np.float64) # we can specify dtype
b = np.array([[7,8], [9,10], [11, 12]], dtype=np.float64)
c = a.dot(b)
print (f"{a.shape} · {b.shape} = {c.shape}")
print (c)





(2, 3) · (3, 2) = (2, 2)
[[ 58.  64.]
 [139. 154.]]



Axis operations


We can also do operations across a specific axis.



axis operations



1
2
3
4
5
6
# Sum across a dimension
x = np.array([[1,2],[3,4]])
print (x)
print ("sum all: ", np.sum(x)) # adds all elements
print ("sum axis=0: ", np.sum(x, axis=0)) # sum across rows
print ("sum axis=1: ", np.sum(x, axis=1)) # sum across columns





[[1 2]
 [3 4]]
sum all:  10
sum axis=0:  [4 6]
sum axis=1:  [3 7]



1
2
3
4
5
6
# Min/max
x = np.array([[1,2,3], [4,5,6]])
print ("min: ", x.min())
print ("max: ", x.max())
print ("min axis=0: ", x.min(axis=0))
print ("min axis=1: ", x.min(axis=1))





min:  1
max:  6
min axis=0:  [1 2 3]
min axis=1:  [1 4]



Broadcast


What happens when we try to do operations with tensors with seemingly incompatible shapes? Their dimensions aren’t compatible as is but how does NumPy still gives us the right result? This is where broadcasting comes in. The scalar is broadcast across the vector so that they have compatible shapes.



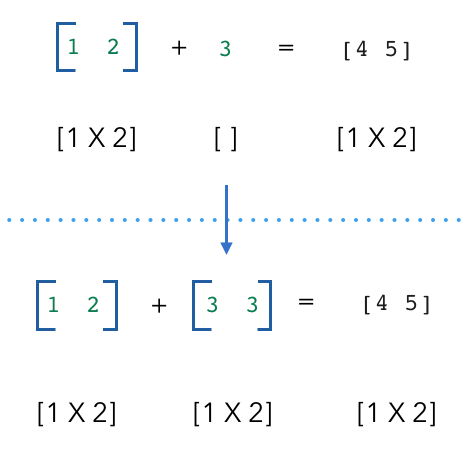
numpy broadcasting



1
2
3
4
5
# Broadcasting
x = np.array([1,2]) # vector
y = np.array(3) # scalar
z = x + y
print ("z:\n", z)





z:
 [4 5]



Gotchas


In the situation below, what is the value of c and what are its dimensions?


1
2
3
a = np.array((3, 4, 5))
b = np.expand_dims(a, axis=1)
c = a + b





1
2
3
4
a.shape # (3,)
b.shape # (3, 1)
c.shape # (3, 3)
print (c)





array([[ 6,  7,  8],
        [ 7,  8,  9],
        [ 8,  9, 10]])



How can we fix this? We need to be careful to ensure that a is the same shape as b if we don't want this unintentional broadcasting behavior.

1
2
3
4
5
a = a.reshape(-1, 1)
a.shape # (3, 1)
c = a + b
c.shape # (3, 1)
print (c)





array([[ 6],
       [ 8],
       [10]])



This kind of unintended broadcasting happens more often then you'd think because this is exactly what happens when we create an array from a list. So we need to ensure that we apply the proper reshaping before using it for any operations.


1
2
3
4
a = np.array([3, 4, 5])
a.shape # (3,)
a = a.reshape(-1, 1)
a.shape # (3, 1)





Transpose


We often need to change the dimensions of our tensors for operations like the dot product. If we need to switch two dimensions, we can transpose
the tensor.



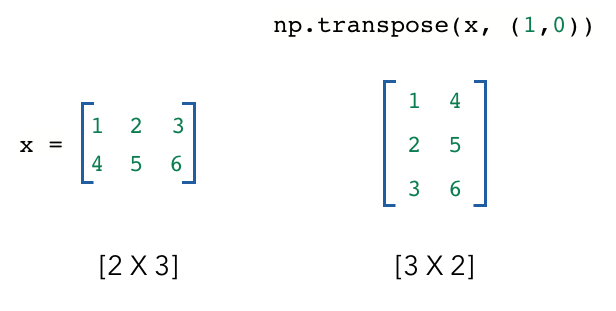
numpy transpose



1
2
3
4
5
6
7
# Transposing
x = np.array([[1,2,3], [4,5,6]])
print ("x:\n", x)
print ("x.shape: ", x.shape)
y = np.transpose(x, (1,0)) # flip dimensions at index 0 and 1
print ("y:\n", y)
print ("y.shape: ", y.shape)





x:
 [[1 2 3]
 [4 5 6]]
x.shape:  (2, 3)
y:
 [[1 4]
 [2 5]
 [3 6]]
y.shape:  (3, 2)



Reshape


Sometimes, we'll need to alter the dimensions of the matrix. Reshaping allows us to transform a tensor into different permissible shapes. Below, our reshaped tensor has the same number of values as the original tensor. (1X6 = 2X3). We can also use -1 on a dimension and NumPy will infer the dimension based on our input tensor.


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
# Reshaping
x = np.array([[1,2,3,4,5,6]])
print (x)
print ("x.shape: ", x.shape)
y = np.reshape(x, (2, 3))
print ("y: \n", y)
print ("y.shape: ", y.shape)
z = np.reshape(x, (2, -1))
print ("z: \n", z)
print ("z.shape: ", z.shape)





[[1 2 3 4 5 6]]
x.shape:  (1, 6)
y:
 [[1 2 3]
 [4 5 6]]
y.shape:  (2, 3)
z:
 [[1 2 3]
 [4 5 6]]
z.shape:  (2, 3)



The way reshape works is by looking at each dimension of the new tensor and separating our original tensor into that many units. So here the dimension at index 0 of the new tensor is 2 so we divide our original tensor into 2 units, and each of those has 3 values.



reshape numpy arrays





Unintended reshaping


Though reshaping is very convenient to manipulate tensors, we must be careful of its pitfalls as well. Let's look at the example below. Suppose we have x, which has the shape [2 X 3 X 4].


1
2
3
4
x = np.array([[[1, 1, 1, 1], [2, 2, 2, 2], [3, 3, 3, 3]],
            [[10, 10, 10, 10], [20, 20, 20, 20], [30, 30, 30, 30]]])
print ("x:\n", x)
print ("x.shape: ", x.shape)





x:
[[[ 1  1  1  1]
[ 2  2  2  2]
[ 3  3  3  3]]


[[10 10 10 10]
[20 20 20 20]
[30 30 30 30]]]
x.shape:  (2, 3, 4)



We want to reshape x so that it has shape [3 X 8] but we want the output to look like this:


[[ 1  1  1  1 10 10 10 10]
[ 2  2  2  2 20 20 20 20]
[ 3  3  3  3 30 30 30 30]]



and not like:


[[ 1  1  1  1  2  2  2  2]
[ 3  3  3  3 10 10 10 10]
[20 20 20 20 30 30 30 30]]



even though they both have the same shape [3X8]. What is the right way to reshape this?



Show answer

When we naively do a reshape, we get the right shape but the values are not what we're looking for.



incorrectly reshaping numpy arrays



1
2
3
4
# Unintended reshaping
z_incorrect = np.reshape(x, (x.shape[1], -1))
print ("z_incorrect:\n", z_incorrect)
print ("z_incorrect.shape: ", z_incorrect.shape)





z_incorrect:
[[ 1  1  1  1  2  2  2  2]
[ 3  3  3  3 10 10 10 10]
[20 20 20 20 30 30 30 30]]
z_incorrect.shape:  (3, 8)



Instead, if we transpose the tensor and then do a reshape, we get our desired tensor. Transpose allows us to put our two vectors that we want to combine together and then we use reshape to join them together. And as a general rule, we should always get our dimensions together before reshaping to combine them.



correctly reshaping numpy arrays



1
2
3
4
5
6
7
# Intended reshaping
y = np.transpose(x, (1,0,2))
print ("y:\n", y)
print ("y.shape: ", y.shape)
z_correct = np.reshape(y, (y.shape[0], -1))
print ("z_correct:\n", z_correct)
print ("z_correct.shape: ", z_correct.shape)





y:
[[[ 1  1  1  1]
[10 10 10 10]]


[[ 2  2  2  2]
[20 20 20 20]]


[[ 3  3  3  3]
[30 30 30 30]]]
y.shape:  (3, 2, 4)
z_correct:
[[ 1  1  1  1 10 10 10 10]
[ 2  2  2  2 20 20 20 20]
[ 3  3  3  3 30 30 30 30]]
z_correct.shape:  (3, 8)





This becomes difficult when we're dealing with weight tensors with random values in many machine learning tasks. So a good idea is to always create a dummy example like this when you’re unsure about reshaping. Blindly going by the tensor shape can lead to lots of issues downstream.








Joining


We can also join our tensors via concatentation or stacking.


1
2
3
x = np.random.random((2, 3))
print (x)
print (x.shape)





[[0.79564718 0.73023418 0.92340453]
 [0.24929281 0.0513762  0.66149188]]
(2, 3)



1
2
3
4
# Concatenation
y = np.concatenate([x, x], axis=0) # concat on a specified axis
print (y)
print (y.shape)





[[0.79564718 0.73023418 0.92340453]
 [0.24929281 0.0513762  0.66149188]
 [0.79564718 0.73023418 0.92340453]
 [0.24929281 0.0513762  0.66149188]]
(4, 3)



1
2
3
4
# Stacking
z = np.stack([x, x], axis=0) # stack on new axis
print (z)
print (z.shape)





[[[0.79564718 0.73023418 0.92340453]
  [0.24929281 0.0513762  0.66149188]]

 [[0.79564718 0.73023418 0.92340453]
  [0.24929281 0.0513762  0.66149188]]]
(2, 2, 3)



Expanding / reducing


We can also easily add and remove dimensions to our tensors and we'll want to do this to make tensors compatible for certain operations.


1
2
3
4
5
6
7
# Adding dimensions
x = np.array([[1,2,3],[4,5,6]])
print ("x:\n", x)
print ("x.shape: ", x.shape)
y = np.expand_dims(x, 1) # expand dim 1
print ("y: \n", y)
print ("y.shape: ", y.shape)   # notice extra set of brackets are added





x:
 [[1 2 3]
  [4 5 6]]
x.shape:  (2, 3)
y:
 [[[1 2 3]]
  [[4 5 6]]]
y.shape:  (2, 1, 3)



1
2
3
4
5
6
7
# Removing dimensions
x = np.array([[[1,2,3]],[[4,5,6]]])
print ("x:\n", x)
print ("x.shape: ", x.shape)
y = np.squeeze(x, 1) # squeeze dim 1
print ("y: \n", y)
print ("y.shape: ", y.shape)  # notice extra set of brackets are gone





x:
 [[[1 2 3]]
  [[4 5 6]]]
x.shape:  (2, 1, 3)
y:
 [[1 2 3]
  [4 5 6]]
y.shape:  (2, 3)





Check out Dask for scaling NumPy workflows with minimal change to existing code.







To cite this content, please use:


1
2
3
4
5
6
@article{madewithml,
    author       = {Goku Mohandas},
    title        = { NumPy - Made With ML },
    howpublished = {\url{https://madewithml.com/}},
    year         = {2022}
}